Regression Analysis

Part 1:

The null hypothesis states, there is no linear association between the crime rate and the percentage of free lunches given out. The alternative hypothesis states, that there is a linear relationship between crime rate and the percentage of free lunches given out. In order to determine whether or not a linear relationship exists between the two variables of crime late and percent free lunches, linear regression analysis is used. The data for each variable was ran through a linear regression analysis using SPSS, with a significance level of 0.05. The results of the analysis provide an equation of the two variables of Y=21.819 + 1.685X where crime rate is the dependent variable represented by Y, and percent free lunch is the independent variable, represented by X. The equation indicates a positive linear correlation explaining that for every one increase in percentage of free lunches, the crime rate in turn increases by 1.685. Therefore predictions can be made using the equation. For example, approximately 34.35 free lunches are given out in areas with a crime rate of 79.7. Although the equation and scatter plot represent a distinguishable positive correlation, the actual linear relationship between the variables is extremely weak as indicated by an R² value of only 0.173, which also makes predictions less accurate. However, based on the results of the regression analysis, the null hypothesis can be rejected because of a significance level less than 0.05, at 0.005. Thus, there is a weak linear association between crime rate and the percent of free lunches given out.

Part 2:

Introduction:

The UW system is curious in determining whether or not certain factors influence the amount of enrollment at two different schools, the University of Wisconsin Milwaukee and the University of Wisconsin Eau Claire. The amount of enrollment at each university may be influenced by factors such as the amount of income and education in certain counties, as well as the distance of each county away from each university. These variables can determine a student’s decision in deciding between different universities, thus affecting the amount of enrollment at different schools. Data regarding the enrollment amount at each university as well as income, percent bachelor’s degree, and distance for each county in Wisconsin is used. In order to determine whether or not these variables influence the amount of enrollment the data is analyzed using regression analysis. After performing regression analysis on the data the UW System can determine which factors are most significant in influencing enrollment amounts at the University of Wisconsin Milwaukee and the University Wisconsin Eau Claire. When significant factors are determined, spatial representations are used in relation to the regression statistics to determine spatial patterns of enrollment based on the most influential variables.

Methodology:  

Regression analysis will determine whether or not to reject the null hypothesis, stating that there is no relationship between each variable and enrollment at both universities. If statistically significant, then the alternative hypothesis, stating there is a linear relationship between each variable and enrollment at both universities, can be investigated. In order to properly determine which variables have the most significant influence on the amount of enrollment at each university the data is analyzed through regression analysis in SPSS.  Regression analysis statistics are performed in SPSS to determine whether or not any of the three suspected variables have a significant relationship to the amount of enrollment at each university. Six different regression analyses are performed using the enrollment data for both universities in relation to each of the three variables. The results each analysis will indicate which variables have significant relationships to the amount of enrollment at each university, thus indicating which factors are more influential on a student’s decision to attended different universities.

The data for the three variables include median household income in each county, percent bachelor’s degrees in each county, and the distance of each county (from its center) away from each university. The data regarding median household income and percent bachelor’s degree for each county are ready for analysis and do not need to be normalized or altered. However, the distance data must be normalized based on the population for a more accurate analysis of the data. This is done by dividing the distance for each county by the population for each county. The normalized distance data will be used in the regression analysis.

Three separate regression analyses are performed using the enrollment data for the University of Wisconsin Eau Claire in relation to each of the three variables. The regression analysis will indicate whether or not there is a relationship between each variable and the enrollment amount at Eau Claire as well as create an equation of the relationship providing a means to make predications regarding that relationship.  The goal is to establish whether or not the enrollment amount at the university depends on variables such as income, percent bachelor’s degrees, and distance. Because of this the enrollment data for this university is used consistently as the dependent variable in order to determine how the other variables, the independent variables, influence enrollment amount. After three separate regression analyses were performed comparing the University of Wisconsin Eau Claire enrollment data to the suspected independent variables, the same was done using the University of Milwaukee enrollment data compared to the same three independent variables. The results of each regression analyses in SPSS will indicate which variables have a significant relationship with the enrollment amounts at each university as well as the pattern of that relationship in the form of an equation.

After the regression analysis provides the statistics determining the most significant variables, the data for those variables can be graphed in relation to the enrollment data for each university. The graphs will provide a visual interpretation of the trends associated with each significant variable. A scatterplot will display the actual pattern of the raw data in comparison to a trend line with an equation determined by regression analysis. The observed data plotted in comparison to a trend line representing the predicted relationship helps to visually identify both the pattern and strength associated with the relationship of a given variable with the amount of enrollment at both universities.       

In order to better understand the most influential factors, spatial representations of each significant variable are produced to be examined in relation to the regression statistics. The spatial representations map the residuals of the statistically significant variables. The residuals indicate the amount the actual data deviates from the predicted value of the relationship provided by the equation. Residuals that are closer to zero indicate no deviation of the actual data to the predicted outcome, meaning a relationship between variables can be accurately predicted. The further the residual is from zero in either direction indicates a less accurate prediction of a relationship. The residuals for each county for the significant variables can be saved in SPSS during regression analysis to be used in ArcMap. The maps created in ArcMap of the residuals help identify which counties in Wisconsin are accurate representations of specific factors influencing enrollment at each university, and which counties appear as outliers. Establishing areas where outliers are occurring allows for a clearer interpretation of certain patterns regarding the influence of specific factors on enrollment at each university. 

Results:

Based on the results of the regression analyses comparing the Enrollment amount at the University Wisconsin Eau Claire and each of the three variables, two of the three variables were found to be statistically significant. The null hypothesis is rejected regarding both percent bachelor degrees and the distance variable. Therefore, there is a significant linear association between percent bachelor’s degrees and Eau Claire enrollment as well a significant relationship between distance and enrollment. The null hypothesis is rejected for both these variables considering the regression analysis provided statistics with a significance level below 0.05. However, the variable regarding income did not show a significant association to enrollment at Eau Claire after regression analysis. A significance level for this variable greater than 0.05 fails to reject the null hypothesis, meaning there is not a significant linear relationship between median house hold income and Eau Claire enrollment.

 

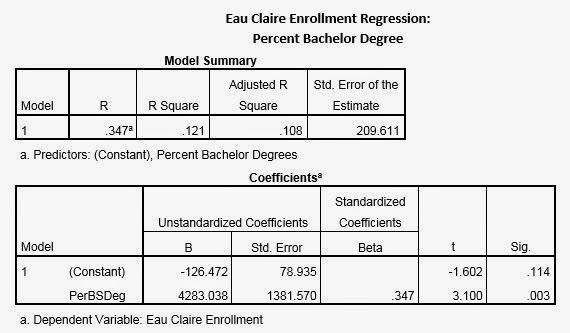
After establishing which variables are significant in regards to influencing enrollment at Eau Claire, further analysis of the regression statistics provides information about the strength and direction of that relationship. In regards to the influence of percent bachelor’s degrees on Eau Claire enrollment, the relationship provided by an equation of Y=-126.472+4283.038X and an R² of 0.121 indicates a weak but apparent positive linear association. Thus, for every one increase in percentage of bachelor’s degrees enrollment at Eau Claire increases by approximately 43 students. However, even though the relationship is proved to be statistically significant the predictions that can be made provided by this equation are fairly inaccurate considering the R² of 0.121 is relatively low, representing a weak relationship. On the other hand, the distance variable not only proves to be statistically significant, but the relationship between distance and enrollment is much stronger. The equation of Y=8.518+0.124X and an R² value of 0.945 indicates a strong positive relationship between the two variables. As the distance increases, enrollment in turn increases at a rate of 0.124. Where counties 500 miles away have a typical enrollment of 70 students at Eau Claire. Predications that are made using the equation for this variable are fairly accurate considering the strong relationship provided by the R² value of almost 0.945, but the rate of increase is fairly minimal.

 

Based on the results of the regression analyses comparing enrollment amounts at the University of Wisconsin Milwaukee and each of the variables, all three of the variables were proved to be statistically significant. Because of a given significance level of less than 0.05 in all the results we can reject the null hypothesis concerning all three variables. Therefore, there is linear association between Milwaukee enrollment and distance, as well as linear relationship between Milwaukee enrollment and both percent bachelor’s degrees and income. Despite the relevance of all three variables being statistically significant, the strength and pattern concerning each relationship still needs to be examined.  

The relationship between median house hold income and Milwaukee enrollment is the weakest of the three relationships. The equation of Y=-1006.75+0.039X created through regression analysis displays a positive linear relationship between income and enrollment. For every increase in median house hold income, enrollment increases by 0.039. A median household income of around 30,000 for a county contributes to about 164 students at Milwaukee. Despite the ability to make predictions of the influence of income on enrollment using the equation, the R² value of 0.068 indicates a very weak relationship between the variables making predictions less accurate. 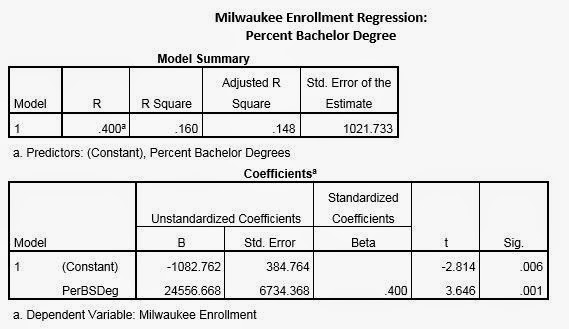The relationship concerning the influence of percent bachelor’s degrees on Milwaukee enrollment shows a slightly stronger relationship. Although the relationship between the variables is slightly stronger than the last, it is still fairly weak as indicated by an R² value of 0.16. The equation of Y=-1082.762+24556.66X explains a positive linear relationship, where for every one percentage increase in the amount of bachelor’s degrees, enrollment increases by about 245 students. Predictions made from this equation will likely be inaccurate concerning the weak relationship between the variables. However, the relationship regarding the influence of distance on enrollment at Milwaukee has a much stronger linear association. The R² value of 0.922 identifies a strong association between the variables and the equation of Y=108.041+0.015X shows a positive relationship. For counties 500 miles away there is an enrollment of 115 student and is increasing by 0.015 students per mile away. Predictions concerning the influence of distance on Milwaukee enrollment are fairly accurate taking into consideration the overall strength of the relationship, however the rate of increase of enrollment per increase in distance in minimal.  

 

Further connections can be made when results of the regression analyses are considered in relation to the spatial representations of the residuals for the significant variables. The areas on the maps that display residuals further away from zero can be determined as outliers, meaning those are areas that do not follow the expected prediction given by the equations.

 

The map in the top right displays the residuals from the relationship between Eau Claire enrollment and percent bachelor’s degrees. The counties in green represent areas with residuals closest to zero, meaning they follow the predicted pattern on the amount of influence of bachelor’s degrees on enrollment. However, the counties in blue and yellow would be considered outliers. These counties do not display the predicted amount of enrollment at Eau Claire based on the percentage of bachelor’s degrees in those counties. Therefore, the percentage of bachelor’s degrees in those counties do not have the same influence on enrollment at Eau Claire compared to the green counties. The map to the top left displays the residuals of the relationship between distance and Eau Claire enrollment. The counties that follow the predicted pattern of enrollment influenced by distance are displayed in light blue. These are the counties that have residuals much closer to zero, which means those are the counties with accurate representations of the predicted influence of distance on Eau Claire enrollment. The other counties, do not follow the predicted pattern indicating that the distance factor does not influence enrollment at Eau Claire.

The maps on the bottom are displays the residuals of the relationship between the University of Wisconsin Milwaukee and each of the three significant factors. The map on the bottom right shows the residuals of the relationship between percent bachelor’s degrees and enrollment. In this map, the residuals in green are the ones closest to zero making those counties ones that are accurate predictions of the influence of bachelor degrees. The light blue counties, like the green, are also fairly accurate. However, the counties in dark blue and yellow are the counties where the percent bachelor’s degrees do not provide an accurate representation of the enrollment at Milwaukee, and that the influence of bachelor’s degrees in these areas is not as strong. The map in the center portrays the residuals of the relationship between distance and Milwaukee enrollment. Majority of the state, shown in yellow, follow the predicted pattern of the influence of distance on enrollment considering those are the counties with residuals closet to zero. There are a select few counties, particularly the ones in blue, with residuals much higher than zero, meaning distance in not a significant influence in those areas and cannot be used to accurately determine enrollment. The last map shows the residuals for the relationship between income and enrollment. Much of the map, in green and some yellow, indicate that income is a predictable factor of influence for determining enrollment in those counties. There are, however, a couple of outliers in blue indicating income is not an influential factor contributing to Milwaukee enrollment.   

Conclusion:           
When considering the statistics as well as the residual maps conclusions can be made about influential factors determining enrollment at different schools. Not only can the statistics determine which factors are statistically significant and have the most influence but they also provide information concerning the pattern and strength of the influence. This information is particularly helpful when used in relation to the residual maps, as certain significant factors of influence vary based on location. Overall, the statistics can provide the means to determine which factors are most influential, but the maps allow clearer interpretation of where each variable has the most influence. Some factors deemed the most influential in determining enrollment at different schools are more significant in some counties compared to others. Because of this different areas seem to be more influenced by one variable, and may not be as influenced by another.

The most significant factors influencing enrollment at the University of Eau Claire include the percentage of bachelor’s degrees in each county as well the distance away from the university. Even though both of these factors have a statistically significant relationship with the amount of enrollment, the influence varies on a county level. When considering the influence of the percent bachelor’s degrees it is clear that much of the state follows the predicted pattern associated with the relationship to enrollment. Thus, much of these areas indicate that the amount of bachelor’s degrees has a predictable influence on enrollment. However, certain areas in the center of the state along with a few counties to the north do not follow the predicated relationship between bachelor degrees and enrollment. Because of this the influence of the amount of bachelor’s degrees on enrollment is not as strong in these areas. In contrast, the same counties, along with a few others, are clearly influenced by distance and have a strong connection to the pattern associated with the relationship between distance and enrollment. Coincidentally much of the counties that follow this pattern are near the University of Wisconsin Eau Claire, therefore it is not surprising to conclude distance is an influential factor in these areas.

The most significant factors which influence the enrollment at the University of Wisconsin Milwaukee include, percentage of bachelor’s degrees in each county, the median income in each county, as well as distance away from the university. Much of the state is equally influenced by percentage of bachelor’s degrees in the sense that most counties follow the pattern associate with the relationship, as shown by the residual map. However, Milwaukee County does not follow the same pattern as the rest of the state, where the influence of bachelor’s degrees on enrollment is minimal, and that other factors have much more influence in this county. Similar the lack of influence associated with bachelor’s degrees on enrollment in Milwaukee County, income is another factor that is not as influential. Much of the rest of the state has a predictable enrollment amount associated with the influence of income, however Milwaukee County does not. The influence of distance in Milwaukee County, on the other hand, appears to be the most predictable influence on enrollment.

Based on analysis of all the data, it is easy to determine that the most significant factor influencing enrollment at both university is distance. When considering how other significant factors influence enrollment at each university, the influence is not the same throughout the state. While some counties may be more influenced by the percentage of bachelor’s degrees other counties, specifically the ones closer to the university, are more influenced by distance.

Correlation and Spatial Autocorrelation Analysis

Part 1:

The Null hypothesis states there is no linear association between distance and sound level. The Alternative hypothesis states there is a linear association between distance and sound level. The Pearson correlation statistic was calculated using a two tailed test and a significant level of 0.05. The correlation calculation shows a value of -0.896 which represents a strong negative relationship between distance and sound level. The Null hypothesis is rejected, stating there is a linear association between distance and sound. As distance increases, the sound level in turn decreases. 

Correlations
		PerWhite	PerBlack	PerHis	NO_HS	BS	BELOW_POVE	Walk
PerWhite	Pearson Correlation	1	-.887**	-.218**	-.532**	.650**	-.767**	.028
	Sig. (2-tailed)		.000	.000	.000	.000	.000	.630
	N	307	307	307	307	307	307	306
PerBlack	Pearson Correlation	-.887**	1	-.246**	.171**	-.503**	.668**	-.050
	Sig. (2-tailed)	.000		.000	.003	.000	.000	.386
	N	307	307	307	307	307	307	306
PerHis	Pearson Correlation	-.218**	-.246**	1	.759**	-.320**	.182**	.029
	Sig. (2-tailed)	.000	.000		.000	.000	.001	.616
	N	307	307	307	307	307	307	306
NO_HS	Pearson Correlation	-.532**	.171**	.759**	1	-.559**	.501**	.050
	Sig. (2-tailed)	.000	.003	.000		.000	.000	.384
	N	307	307	307	307	307	307	306
BS	Pearson Correlation	.650**	-.503**	-.320**	-.559**	1	-.521**	.081
	Sig. (2-tailed)	.000	.000	.000	.000		.000	.157
	N	307	307	307	307	307	307	306
BELOW_POVE	Pearson Correlation	-.767**	.668**	.182**	.501**	-.521**	1	.354**
	Sig. (2-tailed)	.000	.000	.001	.000	.000		.000
	N	307	307	307	307	307	307	306
Walk	Pearson Correlation	.028	-.050	.029	.050	.081	.354**	1
	Sig. (2-tailed)	.630	.386	.616	.384	.157	.000
	N	306	306	306	306	306	306	306
**. Correlation is significant at the 0.01 level (2-tailed).

        The correlation matrix provides statistical evidence for a variety of positive and negative correlations between race, education, and poverty in Milwaukee County. For instance there is slight positive correlation (Pearson Correlation = 0.65) identifying as the percentage of white population increases, there is also an increase in the number of bachelor’s degree in that area. This correlation may also be reflective of the strong negative association (Pearson Correlation = -0.767) indicating as the white population percentage increases in an area, the amount of people below the poverty line decreases. Furthermore there is a fairly strong positive correlation between percentage of black population in an area and the amount of individuals below the poverty line. The correlation statistic (Pearson Correlation = 0.668) portrays a trend of similar increase in poverty with increase in percentage of black population. In addition to the black and white percentage population correlations with education and poverty there is also a strong positive correlation statistic (Pearson Correlation = 0.759) between percent Hispanic population and the amount of individuals without a high school diploma. This correlation shows that areas with high Hispanic populations correspondingly are areas with high amounts of individuals without high school diplomas. Not only do percentages of a particular race in certain areas show associations with education and poverty, but there is also a noticeable correlation between the amount of individuals who walk to work and individuals below the poverty line. This correlation (Pearson Correlation = 0.354) shows as the number of individuals below the poverty line increases, the amount of individuals walking to work somewhat increases in a similar way.

 The correlation matrix has provided statistical evidence to find associations between several distinct factors. The Pearson Correlation numbers show evident connections to increases in poverty in correspondence to certain races, as well as decreased amounts of education with those races. Not only was poverty and education shown to have a noticeable associations between different races, but the statistics also identified an obvious connection between education and poverty as well. 

Part 2:

Introduction:

The Texas Election Commission is interested in analyzing election patterns for the state of Texas throughout the last 20 years. The state of Texas is predominantly concerned about clustering of particular voting patterns and whether or not these patterns have remained consistent over the last 20 years. Percent democratic vote and voter turnout data for both 1980 and 2008 elections have been analyzed to determine whether or not clustering is occurring in Texas, as well as if similar voting patterns are consistent over 20 years. Furthermore, the Texas Election Commission wants to know, if clustering is occurring, whether or not certain population variables influence certain patterns. Therefore data regarding percent Hispanic population in Texas has been used in relation to the voting data, considering Texas’s significant Hispanic population. After statistical and spatial analysis of the data, the Texas Election Commission is able to provide identifiable voting pattern information to the governor.

Methodology:

In order to efficiently identify whether or not clustering of certain voting patterns is occurring, and if these patterns are consistent over time, data is analyzed through spatial autocorrelations. Spatial autocorrelation analysis produce a spatial representation which can be used to identify whether or not the distribution of a variable indicates a systematic pattern over space. If clustering is occurring in voting patterns in the state of Texas, spatial autocorrelation will portray, not only if there is clustering or not, but also the areas in which clustering is occurring. Texas Election commission is also interested whether or not certain population variables influence possible clustering patterns. In addition to the percent democrat vote and voter turnout for 1980 and 2008, the percent Hispanic population is taken into consideration to examine if any relationship exists between certain voting patterns and fairly dense Hispanic population in Texas.   

The data obtained through the Texas Election Commission provides information for the percent democratic vote and the voter turnout for both 1980 and 2008. The data for the 2010 Hispanic population was obtained through the US census bureau.  In order to run spatial autocorrelations on all five of these variables, the data must be linked to a shapefile in order to produce a spatial representation. Once the data for all the desired variables are combined and joined to the shapefile of all the Texas Counties spatial autocorrelation maps can be produced using Geoda. The shapefile connected to the data for each variable can be uploaded into Geoda, where various autocorrelation statistics can be ran. In Geoda, both a Moran I scatter plot and a LISA cluster map were created for: percent democratic vote in 1980, percent democrat vote in 2008, voter turnout in 1980, voter turnout in 2008, as well as the percent Hispanic population in 2010.

The Moran I calculation compares the value of a variable at any one location with the value at all other locations and produces a number between -1.0 (weak clustering) and 1.0 (Strong Clustering) which determines the strength of the autocorrelation. Not only can Geoda produce a Moran I statistic, it also produces a scatterplot of four quadrants indicating where each observed value for the tested variable lies. Quadrants range from areas of with high values surrounded by areas of other high values of a certain variable (Quadrant I), to areas of low values surrounded by areas of other low values (Quadrant III), as well as areas of high values surrounded by areas of low values (Quadrant II), and areas of low values surround by areas of high values (Quadrant IV). Because areas closer to one another tend to be more similar than areas further away, most of the observed values for a variable will fall within quadrant I and III of the scatterplot. Values of a variable that fall within quadrant II and IV tend to indicate outliers in a situation, representing areas that are unlike the surrounding areas.  The Moran I statistic is helpful in determining the strength of clustering patterns for certain variables, where the scatterplot helps identify details concerning clustering patterns.

The LISA cluster map is also generated through Geoda, and can be used in relation to the Moran I calculation. A cluster map was created for each variable which identifies specific areas where clustering of a particular variable are significant. The cluster map incorporates the placement of the value on the Moran I scatterplot and displays the exact locations of areas of high and low values in comparison to one another. The map helps to identify exactly where clustering occurs by representing where the areas of high values and areas of low values are located, as well as the location of certain outliers. After the Moran I calculation provides evidence for significant clustering, the LISA cluster map can put into perspective where the clustering is actually occurring.

In addition to spatial autocorrelation statistics represented through Moran I scatterplots and LISA cluster maps, simple correlation statistics are also useful in order to determine any relationship between certain variables. Significant correlations between certain variables, particularly between the percent Hispanic population and specific voting patterns, are useful for determining why clustering is occurring. A correlation matrix run through SPSS provides the correlation statistics comparing each of the five variables to one another in order to identify if of the variables has a strong linear relationship to one another. If there are significant correlations between certain variables, then those correlations can possibly explain the reason for certain voting patterns and clustering.

Results:

The data for the first variable of percent democratic vote in 1980 produced a fairly strong Moran I statistic of 0.5752. This statistic indicates there is evident clustering of percent democratic vote throughout the state of Texas in 1980. The Scatterplot produced in relation to the Moran I statistic reflects clustering of areas with high democratic votes surrounded by other areas of high democratic votes along with areas of low democratic votes to other areas with low democratic votes. The LISA cluster map portrays precisely where these high and low democratic voting areas in 1980 are located. The areas with a clustering of high democratic vote are apparent in the southernmost part of the state, along with a few areas to the eastern part of the state. The areas with very low democratic vote are located predominantly to the north and mid-western part of the state.

The data for the variable related to the percent democratic vote in 2008 produced similar results to the 1980 data in both the Moran I scatterplot and LISA cluster map. The Moran I statistic for democratic vote in 2008, though similar to the 1980 data, shows a slightly stronger spatial autocorrelation at 0.6957. The clustering in 2008 is slightly more apparent than in 1980, however areas of high democratic votes seem to still be surrounded by other areas of high democratic vote, and areas of low democratic vote are still surrounded by other areas of low democratic vote. In addition to the similarity between the Moran I statistics between 1980 and 2008, the location of clustering for democratic vote is also similar. It is still apparent that clustering of high democratic vote is still located towards the southernmost part of the state and areas of low democratic vote are primarily towards the northern part of the state.

The second variable concerning the data for voter turnout in 1980 was also analyzed through a Moran I scatterplot and LISA cluster map in order to identify noticeable clustering patterns. The results obtain through the Moran I calculation of 0.4681 indicate there is a considerable clustering pattern occurring in the state of Texas in regards to voter turnout in 1980. The scatterplot indicates significantly more outlier areas present for the voter turnout variable compared to the percent democrat vote variable. However, majority of the data represents clustering of areas of high voter turnout next to other areas of high voter turnout along with clustering of areas of low voter turnout surrounded by other areas of low voter turnout.  The LISA map displays the exact locations where this clustering is occurring. The locations where there is consistent high voter turnout are primarily located at the northernmost part of the state, with a few areas towards the center of the state. The map also indicates the vast areas of low voter turnout are located at the southernmost part of the state, as well as a small area toward the midwest part of the state.

 

The voter turnout data for 2008 shows similar clustering patterns compared to 1980 in both the Moran I scatterplot and LISA cluster map. The Moran I value of 0.364 for voter turnout in 2008 is slightly less than of the Moran I value for 1980. Though the value indicates there is evident clustering occurring for voter turnout in 2008, the clustered areas for high voter turnout and low voter turnout are not as dense compared to 1980. The LISA cluster map for voter turnout displays clustered areas that are comparable to 1980. Even though there is noticeable clustering of high voter turnout in the northern part of the state during the 2008 election, in 1980 the northern part of the state had a much more expansive area of high voter turnout. There is still similar clustering of high voter turnout in various areas of central Texas in 2008 just as there was in 1980. In addition to similar clustering patterns for high voter turnout from 1980 to 2008, there is also consistent pattern for low voter turnout in the southern part of Texas. In 2008, southern Texas maintained significant area of low voter turnout, just as it did in 1980.

The final variable analyzed through a Moran I scatterplot and LISA cluster map was data concerning the percent Hispanic population throughout Texas in 2010. This data was used to identify if clustering of the Hispanic race is comparable to the identifiable clustering of certain voting patterns.  The Moran I value of 0.78 indicates an extremely strong clustering pattern of the Hispanic population.  There are very apparent clustering patterns of highly populated Hispanic areas as well as areas with very low Hispanic populations as indicated by the Moran I scatterplot.  The LISA cluster map portrays the specific areas where high clustering of Hispanic population are present, and the areas where Hispanic population is very low. The map shows the entire southern part of Texas, along the Texas and Mexico border, there is a widespread area of high Hispanic population. In Contrast to this area, the north western part of Texas shows a vast area of very low Hispanic population. These clustering patterns can be examined in relation to particular clustering in voting patterns to indicate whether or not there is a relationship between the Hispanic population and particular voting patterns.

 

In addition to comparing the Moran I scatterplots and LISA cluster maps to identify a relationship between Hispanic population and voting patterns, results from a correlation matrix help solidify any observable relationships. The correlation matrix produced several statistically significant relationships between certain variables.  The Pearson correlation statistic was statistically significant when comparing percent Hispanic population to all voting pattern variables, with expectation the percent democrat vote in 1980. The correlation statistic of 0.699 and significance level of 0 show a strong positive relationship between percent Hispanic vote and percent democrat vote in 2008. This indicates that the areas with higher clustering of Hispanic population are strongly related to the clustering of areas with high democratic votes. In addition to percent democratic vote there is also a strong relationship between Hispanic population and voter turnout in both 1980 and 2008. In both sets of election data a strong negative correlation is present, where in 1980 a correlation statistic of -0.47 was produced, and in 2008 a statistic of -0.668. These statistics are comparable to the cluster maps, indicating areas with high Hispanic population are sequentially areas with low voter turnout.

Conclusion:

The vast majority of the results indicate there is a definite clustering of certain voting patterns occurring in the state of Texas. Not only are clustering of voting patterns occurring, they also appear to remain consistent over time. The southern part of Texas shows a clustering of a high percentage of democratic votes in 1980. This clustering pattern for democratic votes has remained fairly consistent into 2008, and in fact appeared to expand further along with southern border. There is also an identifiable clustering pattern of low democratic in the northern part of Texas that has remained fairly consistent between 1980 and 2008. Strong clustering patterns are also evident in areas regarding voter turnout. The southern part of Texas seems to have maintained a pattern of low voter turnout from 1980 to 2008. These results suggest the occurrence of consistent clustering patterns where southern Texas is predominantly more democratic and has less of a voter turnout, and northern Texas is less democratic and has a significantly strong voter turnout.

In addition to these consistent patterns there is also a strong correlation between the percent Hispanic population in Texas and both percent democratic vote and voter turnout. The statistics indicate areas with larger Hispanic populations are also areas where there are a higher percentage of democratic votes in 2008. Both variables portray strong clustering along the southern border of Texas. The results of the correlation statistics also show a strong relationship to percent Hispanic population and voter turnout in both 1980 and 2008 elections. The results indicate areas with high Hispanic populations are similarly areas with low voter turnout. Both these variables, once again, fall along the southern Texas border. The results specify a strong relationship between Hispanic population and particular voting patterns, which is comparable to the cluster maps portraying southern Texas as an area of high Hispanic population and similarly an area of high percent democratic vote, as well as low voter turnout.  Overall, the results are conclusive in both supporting the idea that the Hispanic population in Texas has a significant influence in particular clustering of voting patterns.